The Boolean expressions govern the mathematical principles behind logic gates. These expressions can be simplified mathematically with the help of Boolean identities, resulting in simpler logic circuits instead of complex ones. This article describes mathematical laws along with a few examples of the application of boolean algebra simplification.

Boolean Algebra Simplification

Boolean algebra simplification is the reduction of variables and operators in a complete Boolean expression. The mathematical identities range from simple to complex theorems. However, every complex function can be split into AND forms and OR forms.

Boolean identities applicable on AND as well as OR forms below tabulated mathematical laws:

Based upon the above laws, we can simplify every complex Boolean expression to a minimal number of terms so the resultant equivalent logic circuit can be drawn in the simplest form.

Example 1

Convert below two stages-based logic gates circuits into a simpler logic circuit using Boolean algebra simplification.

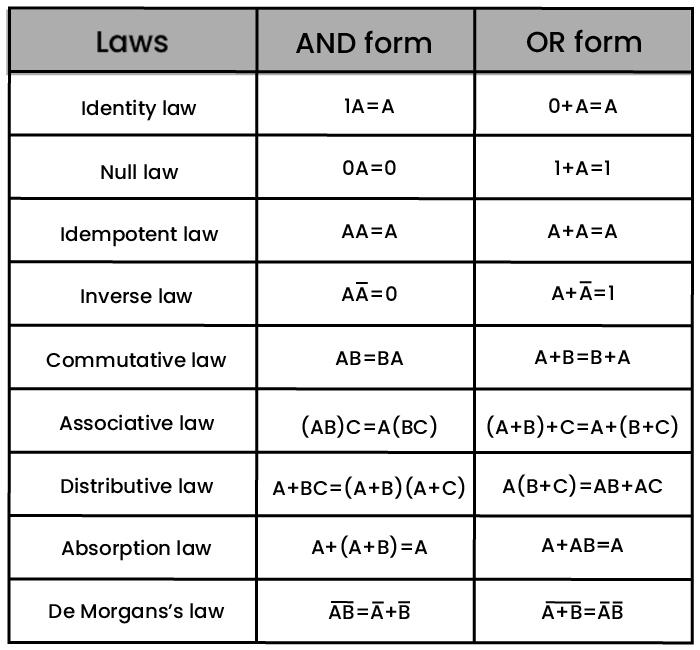
Boolean Expression: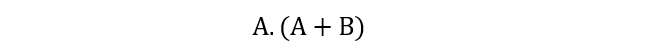
The above Boolean expression implies two stages of logic gates operation. The logic circuit could be drawn as an OR gate with two inputs, and another AND gate operation from the output of the OR gate with the first input.

However, this complex circuit can easily be avoided if we apply the Boolean identities to reduce the number of terms as shown below steps:

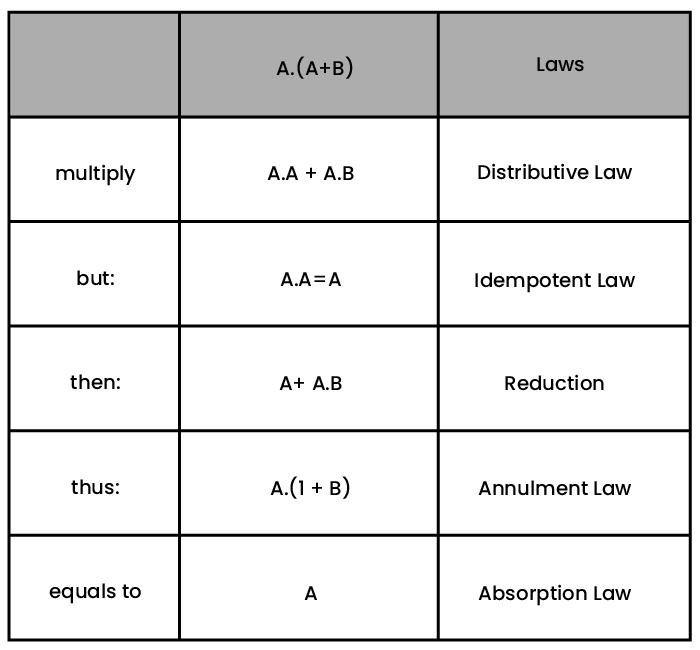
The above five Boolean identities comprising distributive law, idempotent law, reduction, annulment, and absorption laws have simplified the complex circuit to single input expression A. Therefore:

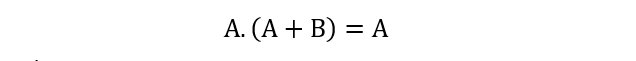
Example 2

Convert below two stages-based logic gates circuits into a simpler logic circuit using Boolean algebra simplification.

Boolean Expression:

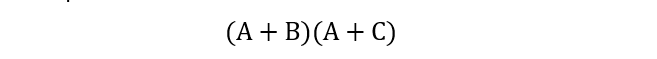
The above Boolean expression is also a two-stage gate operation circuit. First, two inputs based on two OR gates shall be drawn along with further AND gates operation on outputs from these OR gates.

We will make use of Boolean identities to make the above complex logic circuit into a simpler one:

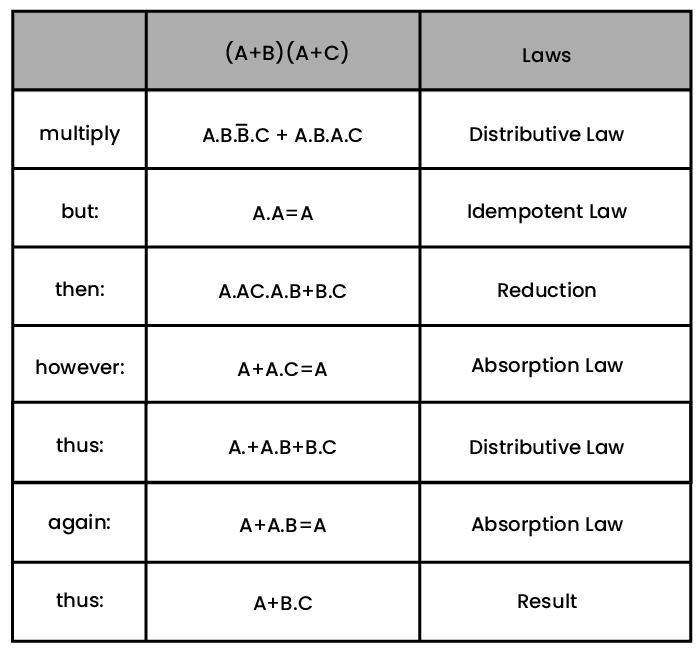
Seven Boolean identities comprising distributive law, idempotent law, reduction operations, and absorption law have reduced the complex circuit into AND & OR operation of three inputs given by:

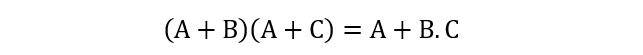
Example 3

Convert below multiple stages-based logic gates circuit into a simple single-stage logic circuit using Boolean algebra simplification.

Boolean Expression:

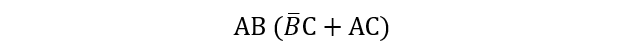
The above is three stage complex logic circuit comprising AND operation in first step, OR gate in second step and finally another AND operation of obtained output with another two inputs can be simplified as below:

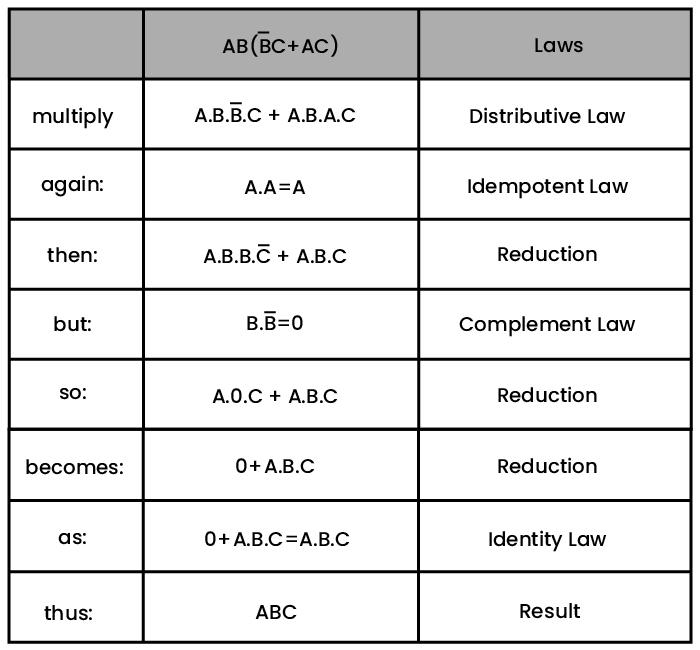
The above eight Boolean simplifications using Boolean identities have now simplified the circuit into a single AND gate with three inputs. Therefore, we can re-write the Boolean expression now:

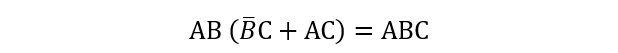
Example 4

Convert the multiple stages-based logic gates circuit into a simple single stage logic circuit using Boolean algebra simplification.

Boolean Expression:

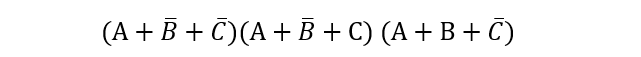
The above expression shows logic gates operations of three numbers of three input OR gates with one or two complement inputs and finally the three AND gates operation on obtained inputs.

The logic circuit drawn for the present expression would be a complex two stages based on three input gates operations. The same can be simplified to reduce number of terms and gates by following below steps:

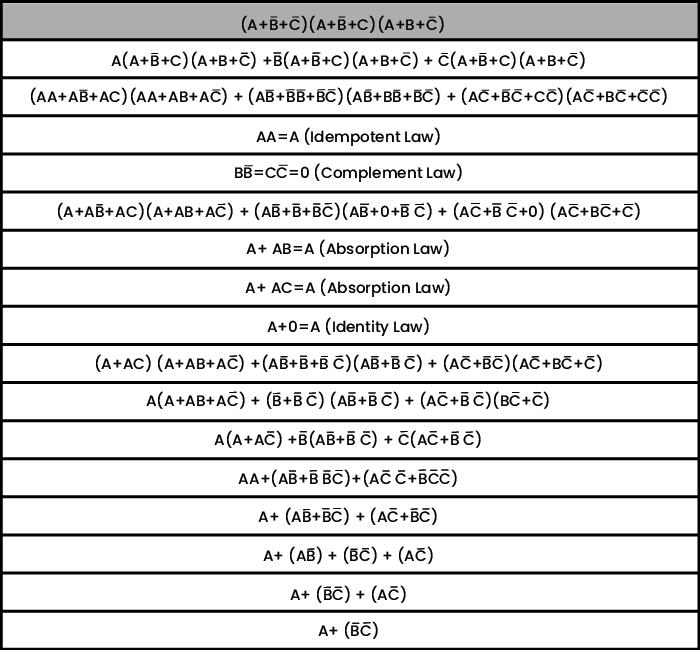
The above expression has been reduced to its simplest form using the associative law of multiplication, idempotent law, complement law, absorption law, identity law, and a few mathematical substitution operations as shown above. Therefore, the above Boolean expression works in the same way as the final simple form, and we can rewrite it as below:

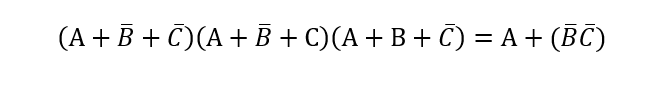Conclusion

The Boolean simplification can convert any complex logic circuit into an alternate simple circuit, reducing the number of logic gates as well as the complexity of Boolean algebra involved in evaluating the outputs. The simple circuit works to provide exactly the same outputs as would the complex circuit in every scenario. This principle can also be proved by comparing truth tables of the two circuits.