SciPy Optimize Curve_fit

May 11, 2023 | by Arround The Web | No comments

Python is a useful tool for fitting data to the desired functional form and is also used to calculate the standard error for any argument in a function fit. In Python, to find the best fit of data, and the optimal set of parameters for any user-defined function, the “curve_fit()” method can be used that enables flexibility.

In this guide, we will explain:

What is “SciPy” in Python?

The “SciPy” stands for “Scientific Python” which is the scientific computation open-source library and uses under the “NumPy”. It provides different utility functions for signal processing, stats, and optimization, such as “NumPy”.

What is “Optimize Curve_fit” in Python?

To get the best-fit parameter, the “Optimize Curve_fit” function can be used in Python. To obtain the optimized parameter for a provided function that fits the specified dataset, the “curve_fit()” function can be used. It is the freely available library in SciPy that is utilized to fit curves using the nonlinear least squares.it takes the input data, output data, and the desired function name that is to be employed.

How to Use Python’s “curve_fit” Function to Fit Data?

To fit any provided data set, first, import the required libraries, such as “numpy”, “matplotlib.pyplot”, “curve_fit”, and “warnings”. Then, specified the state of warning as “ignore”

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
import warnings
warnings.filterwarnings('ignore')

Next, we have created the x-axis and y-axis values for a plot. Then, call an “np.asarray()” function and pass the previously created data to generate an array. After that, call the “plt.plot()” function with created arrays as parameters and the style of line in which we want to display the plot:

xaxis = [-5.0, -4.0, -3.0, -2.0, -1.0, 0.0, 1.0, 2.0, 3.0, 4.0, 5.0]
yaxis = [ 11.7, 13.5, 14.5, 15.7, 16.1, 16.6, 16.0, 15.4, 14.4, 14.2, 12.7]

xaxis = np.asarray(xaxis)
yaxis = np.asarray(yaxis)
plt.plot(xaxis, yaxis, 'o')

Now, we define the “Gaussian” function equation in Python to find the value of “M” and “N” that best fit our data. According to the below-provided code, this function will accept as inputs the x-axis values and all the arguments that will be best fit:

def Gauss(x, M, N):
y = M*np.exp(-1*N*x**2)
return y

Next, call the “curve_fit()” function that takes the function that we need to fit, the values of the x-axis and y-axis as arguments. Then, the optimized values of the “M” and “N” are now saved in the list parameters:

para, covariance = curve_fit(Gauss, xaxis, yaxis)
fit_M = para[0]
fit_N = para[1]

Now, we will calculate the values of the “y” by using our defined function and fit values of “M” and “N”. After that, create a plot to compare those calculated values to our specified data with the “label” parameter with value, function variables, and plot line style. Lastly, call the “plt.show” function to view the resultant plot:

fit_h = Gauss(xaxis, fit_M, fit_N)
plt.plot(xaxis, yaxis, 'o', label='Dataset')
plt.plot(xaxis, fit_h, ':', label='Best-Fit')
plt.legend()
plt.show()

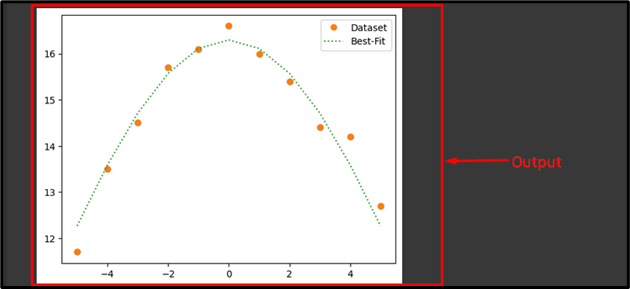
Output

According to the provided output, we have found the best fit for our specified data:

That’s all! We have briefly explained the “curve_fit()” function in Python.

Conclusion

The “Optimize Curve_fit” function is used to get the best-fit parameter in Python and to obtain the optimized parameter for a provided function that fits the specified dataset, the “curve_fit()” function can be used. This guide elaborated on the SciPy Optimize Curve_fit in Python.

Source: linuxhint.com