“Cosine similarity” is a mathematical approach for measuring the similarity of two vectors that are not zero. It is commonly utilized in several fields, including NLP/Natural Language Processing, retrieval of information, and recommendation systems. The “scipy” library provides a function called “cosine()” that can be utilized to determine/calculate cosine similarity between two vectors.

This Python article provides an in-depth guide on “scipy” cosine similarity by covering the following aspects:

• What is Python Cosine Similarity?
• How Does Cosine Similarity Work?
• How to Calculate/Determine Cosine Similarity Using “scipy”?

What is Python Cosine Similarity?

“Cosine similarity” is a way to determine how similar two non-zero vectors are in a space where an inner product exists. The cosine of an angle between two given vectors defines the angle between them. Angles closer to ” 0” degrees are considered to be more similar.

Cosine similarity has a range of “-1” to “1”, with “-1” indicating that the vectors are completely dissimilar and “1” indicating that they are identical. A value of “0” specifies that the vectors are orthogonal “(perpendicular)” to each other.

How Does Cosine Similarity Work?

The “Cosine similarity” works by taking the “dot product” of two input vectors and dividing it by the magnitude product. In order to calculate/determine dot products, the products of corresponding elements in two vectors are added together. The vector magnitude corresponds to the square root of its items/elements’ squares.

Example
The below code uses the “numpy” library to calculate/determine the cosine similarity:

In the above code, the “numpy.dot()” function takes two vectors as its arguments and retrieves the dot product. Similarly, the “norm()” function takes the input vector as an argument and receives the vector norm. It is such that Python calculates cosine similarity by dividing two vectors’ dot products by their norms.

Output

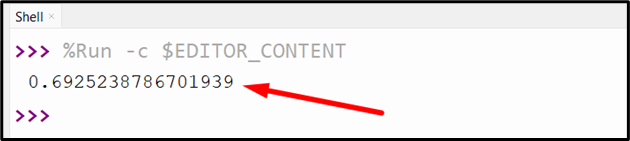
As seen, the “Cosine Similarity” between the input vectors is returned appropriately.

How to Calculate/Determine Cosine Similarity Using “scipy”?

The “scipy” library provides a function called “cosine()” that can be utilized to calculate/determine cosine similarity between two input vectors. This function takes two arrays as its arguments and returns a value between “-1” and “1”.

Example
Let’s overview the following example code:

In this example:

• The “cosine” function from the “scipy.spatial.distance” module is imported at the start.
• The two vectors “vector1” and “vector2” are initialized using the “numpy.array()” function.
• The “cosine similarity” between the two vectors is calculated using the “cosine()” function and subtracts the result from “1” to get the actual similarity value.

Output

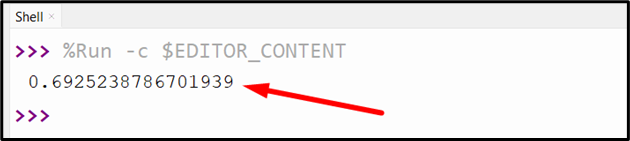
The above snippet returns the cosine similarity between the passed vectors.

Conclusion

“Cosine similarity” is a useful metric for comparing the similarity of two vectors in a high-dimensional space. In this article, we covered the basics of cosine similarity, including how it works and how to calculate it using Python’s “scipy” library.