“The radian is the standard unit of angular reference in the International System of Units (SI), and it is found on the radius of the circle. It is utilized in various branches of mathematics. This indicates that if we envision extending the radius’s extent around a circle, the angle created at the circle’s center by this arc is equal to one radian. It is represented by the symbol rad. The other alternate unit of angle is degrees. Radians and degrees are related in that one degree equal pi/180 radians. This conversion is very often utilized in mathematics or trigonometry fields. Python’s built-in math module has a method to convert degrees to radians which are denoted by math.radians(). The syntax for this method is mentioned below.”

Syntax

The parameter x is a required field which is the value in degrees that has to be converted to radians. In the case in which the parameter is not an integer, the function will return a “Type Error” message.

Example 01

Now we will be implementing the math radian method in the python programming language. As we already know that the radians method is present in the math library, we will have to import this library to use this method in our python program. In this example, we will be using two methods of the math library to provide one result, the pi method and the radian method.

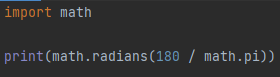
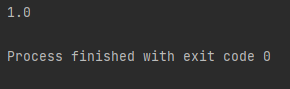
To utilize math package functions in Python, we must first install the math library. In this program, we will directly display the value returned by math.radians(). Inside the print command, we have used this method and passed 180/pi as its parameter. Also, we have used math. pi as the constant value of pi, which is another method of math library to get the accurate or exact value. As we can see in the output below, the result of the function is one because the ratio of 180 and 1 is the mathematical equivalent of one radian, and we have implemented that constant to visualize this phenomenon.

Example 02

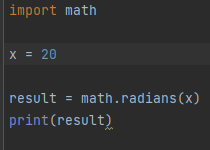
In this example, we will store the degree value of the angle in the variable named “x,” which will be passed on to the math.radians() function. We will initialize our program by importing the math library so that the radians’ function can be used later on in the program. The radian value that is returned by the function is stored in the variable named “result.” The print function is then utilized to show this value, as illustrated in the picture underneath. You can also confirm the answer by using the conversion formula rad = pi/180 * (degrees).

We can see in the output below that the result of the operation is the resultant of the ratio, as we explained in the previous example.

Example 03

Here is another example of the radian’s method with the parameter 180.

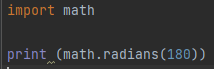
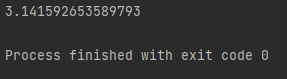
In this program, we are proving the mathematical phenomenon that when the angle of a horizontal line, which is 180 degrees, is converted into radians, it gives the exact value of pi. The print command is used to display the returned value of the math.radians() function, which comes out to be 3.14 (which is the value of pi), as shown in the screenshot below. The answer makes sense as pi/180 *(180) = pi.

Example 04

In this example, we will be using the negative value as the parameter of math.radians() function. First, we import the math library to use this function. Then we pass the value -20 into the function and display it using the print command. It displays the negative value of the angle in radians, which indicates that the angle is formed in a direction that is counter to an arbitrary determined direction, which is usually a clockwise direction.

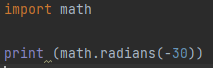
As we can see, the output is a negative angle in the snippet below; this proves that the radians method allows negative values in its parameter and that the radian angle can also be negative.

Example 05

Another way to convert degrees to radians is to import the radians method from the math module.

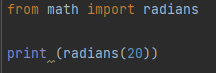
In this program, we will use the alternate approach to import the specific function from a library. We will begin by using the from keyword with the library name and the radians method name; this will let us call the function directly without mentioning the library every time we call the function. As we can see in the image above, we directly called the function and passed a numeric parameter inside it, and displayed the result with the help of the print function, as shown in the screenshot below:

Example 06

In this example, we will learn a new way to use the radians function in python. We will directly import radians from the math library. Now we can use the radians() function rather than the math.radians() object. The parameter will be the same (any numeric value). Moreover, we will use the pi method too by importing the pi constant from the math module in the python programming language. The parameter for the radians() function used is 200/pi (degrees), which returns the radian equivalent value and is displayed at the output terminal using the print command, as shown in the screenshot below.

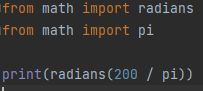
As we can see in the output below, the result of the function is a recursive number just above 1 as the conversion of pi is divided by two hundred, which is a little greater than 180.

Example 07

In the following code, we used a negative value of degrees to be converted into radians by using the radians() method in python. The returned value of the function is printed using the print command, as shown in the screenshot below. The negative sign indicates that the angle is formed in a direction that is counter to an arbitrary determined direction, which is usually in the clockwise direction.

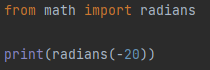
The output below proves further that no matter what we call the function, the parameters and the result of the function can be negative without any modifications.

Example 08

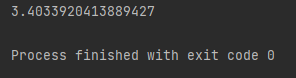
Here is another example of the radians() method. First, we will import radians from the math library in python. Then we stored a numerical value (which is the sum of 15 and 180) in the variable named “a”. This variable is passed to the radians() function as its parameter, and the returned value is stored in the variable “b.” Finally, as demonstrated in the picture underneath, this number is shown using the print method.

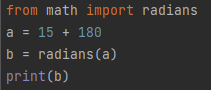
The output below provides us with evidence that a variable that was accumulated by mathematical calculations can also be passed onside the radians method to provide an accurate conversion.

Conclusion

The math module includes functions that are used to calculate the various trigonometric ratios based on a given angle; degrees () and radians() are two such examples that help in the conversion of the angles by simply inputting the angle value, and python itself does all the calculation for us and returns the value in the respective unit. It helps the code appear clear and concise. Code that is both clean and simple is easier to debug and is less likely to include errors. Throughout this tutorial on Python, we learned about converting degrees to radians in Python.