“NumPy is a python package used to deal with arrays, and it uses different built-in mathematical functions. It deals with numerical computation. The numerical computation is going to the advanced level to use mathematical functions in Python, so we need to import NumPy. An important function of NumPy is trapz(); this method has solved multiple problems we have faced in coding. The trapz() method finds the integral along the given axis and interval [a,b]. This function is utilized to find the shaded region of the graph. This method works on the Trapezoidal rule; the trapezoidal is also known as the trapezium or trapezoid rule, which is used for approximating the definite integral. Instead of writing the whole code to find the approximate integral, we can simply use this method to find the integral along the given axis. For example, if we want to find the integral in the program using the trapezium rule, we have to write complete code, but with the trapz() method, we can simply define the axis and values and get the resultant value.”

Syntax

The syntax looks a little tricky, but it is very easy to use once we understand the functionality of all the parameters.

Parameters

• Y: It is the input array or value whose integral we want to find. It is compulsory to give one input to the trapz() method. The value of parameter “y” can be an equation that we want to integrate, but we should define it before using it in the trapz() method.
• X: It is the given sample points that resemble the value of “y.” It is a sampling of y; if we don’t define the x value, it is, by default, none. It is optional. It is array-like but not compulsory to define. When “x” is none, “dx” uniformly splits the sample points.
• Dx: It is the distance between sample points; when dx is not defined by default, it is set to 1. The attribute “dx” equally spaces the sample points.
• Axis: It represents the axis of integration. It should be an integer value, and it is optional.

Return Value

This function will return the estimated definite integral. The return type will be an array or a floating point value.

Integral of 1D Array

In this example, we will observe the functionality of the trapz() method on a one-dimensional array when the array elements are integers.

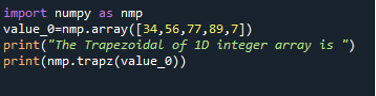
In this code first thing, we have to do is import the numpy library and give a function name. Here the function name is “nmp.” After that, define a variable “value_0” and call the numpy.array() method to use the array function of the numpy module and initialize the one-dimensional array. The array is of integer type, which shows that it has all integer values. Next, a text is printed on the console by declaring the print() function. In the next statement, invoke the nmp.trapz() method. This function contains the “value_0” as the argument. The trapz() method will find the integral of the given array and print that by using print(). We can also store the result of the trapz() function in another variable and then show the result, but that just increases the length of the code, and functionality will remain the same.

The output shows the result of the code, and it is a floating point value. The trapz() method will calculate the integral of the specified array with the trapezoidal formula, and we will just see the outcome.

Integral of a 2-D Array

Now in this program, we will discuss the use of the trapz() function for a two-dimensional array by taking different “dx” values.

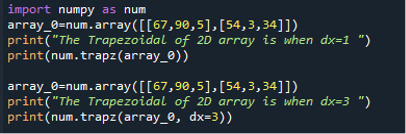
First, integrate the numpy module with any function name. Here the function name is “num.” In the next statement, define a two-dimensional array by using the num.array() function. And save the array elements in the “array_0” variable. Display the text with the print() method. Then we will pass the num.trapz() function to the print statement. The trapz() method has one argument of “array_0”. Here the value of “dx” is, by default, 1.

But in the second portion of the program, the “dx” value is the only thing that differs. Repeat the same code and just change the value of “dx”. Here we specify the value of “dx” as 3. We can now compare the outcomes of both two sections of the above code.

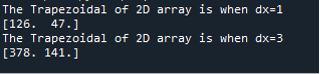
The output clearly shows the difference between both two resultant arrays. The second array is multiplied by 3 because its “dx” is 3; it equally divides the sample points when “dx” is 3.

Integral of Lists

This instance will clarify how to utilize the trapz() method when the input is in the form of lists.

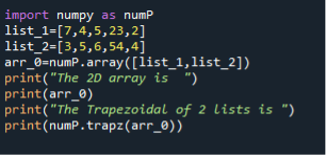
Import the library first. Then initialize two lists; both lists contain integer values. We can initialize the list with floating point values, but here, we use only integer values. Now convert the list into the two-dimensional array by passing the variables of both lists into numpy.array() function. After that, save the resultant array in “arr_0”. Display the message and two-dimensional array on the screen. Further, call the trapz() method to get the integral of the 2D array and show this integral by utilizing the print() function. The “arr_0” contains a two-dimensional array, and trapz() will find the integral of that two-dimensional array.

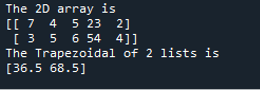
In the outcome, first, we get the message and two-dimensional array that we obtained by converting two lists into a two-dimensional array. Then we get the integral of the array in array format. Remember, the result can either be an array or a floating point value.

Conclusion

In this guide, we have explained the trapz() method in detail. The trapz() method is beneficial because we don’t have to code the formula of this methodology. It is an inbuilt method of the NumPy library. We can call the trapz() method and utilize this function wherever we require it. In the examples, we get the integral of the 1D array, 2D array, and lists. Moreover, we observed the difference in answers when we changed the value of the “dx” argument of the trapz() method. The article covers the trapz() method in depth to make learning easy for you.