We know that complex numbers are those represented by the conventional a+bi, where “a” is always a real number; “b” is also a real number but “i” is an imaginary component. One more thing we know is “i^2 = -1” because none of the real numbers can satisfy this equation which we call “I” an imaginary part. Numpy supports real numbers as well as imaginary numbers. In NumPy, imaginary numbers are represented by “j”. There are various ways to create and manipulate arrays having complex numbers like np.complex(), np.range(), np.array(), and more.

Syntax

The syntax for creating an array that contains complex numbers is as follows:

Method 1:

The syntax given above 1j is the imaginary part which means we are creating an array of complex numbers, where np.arrang is the function that is provided by NumPy to create an array to a specified range. Size, which indicates the array size, is passed to the function.

Method 2:

In this syntax, np.arrray is the function that enables us to create an array but we cannot pass the range to it. We simply pass values to it “n” times. In the function, we passed “Re” which indicates real numbers adding them to “Im” an imaginary number in multiple of a real number. We can pass imaginary values to n times.

Example # 01:

As we know NumPy also supports complex numbers and provides multiple varieties of methods to implement and manipulate complex numbers. In the example below, we will implement two ways to create arrays containing complex numbers. To implement NumPy functions, let us import the NumPy library first as np. Then, we will initialize an array named “array_a” to which we assign the function np.arange() that will contain the complex numbers. And the range of the array will be “8”. In the next line, we created another array named “array_b” to which we passed an array of complex numbers by passing the complex values directly to it. In the end, we printed the complex array that we created using both methods.

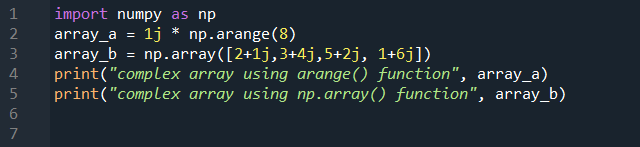
As shown in the snippet below is the result of the code we have executed. We can see that we have created two arrays that have a range of complex numbers from 0j to 7j. In the other one, we have passed the random range of complex numbers of size 4.

Method 3:

In the syntax given above, np.complex() is the built-in class that is provided by the Python package NumPy that enables us to store complex values.

Example # 02:

Another way to create a NumPy complex array is using NumPy’s complex() class. Complex class() is used to store complex numbers and returns the complex object which we can use multiple times within the single code. Now implementing the complex() class, we will first import our Numpy package. Then, we will initialize an array to which we passed a complex class that uses an asterisk “*” to pass an object of complex() class to which we passed “3+1j”. Using the arrange() function, we created an array of size 5. At last, we just displayed the output of the code in which we created a complex array using the complex() class.

As shown in the figure below, we have created an array of complex numbers. But one more thing we can notice in the figure is that the constant value is not being consecutively executed because we have passed “3+1j” to a complex() class which means a number three will be added to every next constant values.

Method 4:

In this method np.ones(), we specify an array of complex numbers using the dtype parameter in the NumPy array. Np.ones() is used to return a new array that contains 1s. To the function np.ones(), we passed four parameters “shape”, which is used to define the shape of the array whether it is “2”, “3” or else. The “dtype” is the data type. In our case we will be using a complex datatype. The “order” defines whether the array is one-dimensional, two, or multi-dimensional.

Example # 03:

Let us implement the ones() method to get a better idea of how it works while using complex numbers. To implement this method, let us first import our packages of NumPy that are provided by Python. Next, we will create an array to which we will pass the np.ones() function to which we passed two parameters. The first one is “4” which means the array size will be 4 and the second one is “dtype” which is complex. This means, we are going to create an array of data type complex numbers. Multiplying the ones() function with the value”2” means our real number will be “2”. In the end, we printed the array that we created using the print statement.

As shown below, the output of our code is executed successfully in which we have a one-dimensional array that contains 4 complex values with a real number 2.

Example # 04:

Let us now implement another example in which we will create an array of complex numbers and will print the imaginary and real parts of the complex numbers. We will first import the NumPy library, then create an array to which we passed “6” complex values to an array named “array” that is “56+0j, 27+0j, 68+0j, 49+0j, 120+0j, 4+0j”. In the next line, we simply printed the array. Now, we print imaginary and real values of the complex array.

Numpy provides a built-in function for both of the operations that are shown below. The first one to get the imaginary part is “array_name.imag” where the value before the dot is the array from which we have to get the imaginary part. And the second one to get the real part is “array_name.real”. In our case, the name of an array is “array” so we passed the print statement, the array name, and the keyword to get both of the elements.

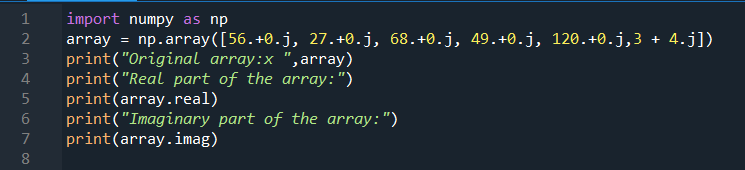
As shown in the snippet below, the output in which the imaginary and the real part of the complex array is successfully executed. Where the real parts are “56”, “27”, “68”, “120”, and “3”. And the imaginary parts are “0’s”.

Conclusion

In this article, we have briefly discussed complex numbers and how we can create complex arrays using NumPy’s built-in functions. We described multiple functions that enable us to create complex arrays by implementing multiple examples to understand better.