The built-in library offered by Python, known as NumPy, allows us to construct the multi-dimensional arrays, modify them, and perform various arithmetic computations on them. Apply function is also provided by the NumPy package. The typical use case for the apply function is similar to the scenario where we want to slice an array and perform some operations on each element of a list, for example, if we want to square off each item of a row. Of course, in Python, we know that for-loops are slow so we would like to avoid them if possible. The “apply” function can be used if you want to do the same operation on each row or column of a data frame. In other words, it does what you want to do with a for-loop without having to write a for-loop.

There are two methods to apply any function to the array depending on the condition. We can apply the “apply over the axis” function which is useful when we apply the function on each element of the array one by one, and it is useful for the n-dimensional arrays. The second method is “apply along the axis” which applies to a one-dimensional array.

Syntax:

Method 1: Apply Along the Axis

In the syntax, we have the “numpy.apply” function to which we pass five arguments. The first one argument which is “1d_function” operates on the one-dimensional array, which is required. While the second argument, the “axis”, is the one on which axis do you want to slice the array and apply that function. The third parameter is “arr” which is the given array to which we want to apply the function. While the “*args” and “*kwargs” are the additional arguments that are not necessary to add.

Example 1:

Moving towards a better understanding of the “apply” methods, we perform an example to check the working of apply methods. In this instance, we perform the “apply_along_Axis” function. Let’s proceed to our first step. We first include our NumPy libraries as np. And then, we create an array named “arr” that holds a 3×3 matrix with integer values which are “8, 1, 7, 4, 3, 9, 5, 2, and 6”. In the next line, we create a variable named “array” which is responsible for holding the result of the apply_along_Axis function.

To that function, we pass three arguments. The first one is the function that we want to apply to the array, in our case it is the sorted function because we want our array to be sorted. Then, we pass the second argument “1” which means we want to slice our array along axis=1. Laslty, we pass the array that is to be sorted in this case. At the end of the code, we simply print both arrays – the original array as well as the resulting array – which are displayed using the print() statement.

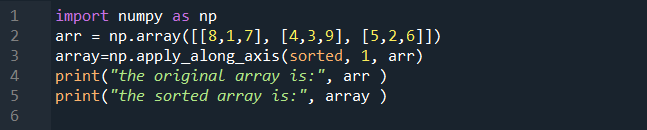
As we can see in the following output, we displayed both arrays. In the first one, the values are randomly placed in each row of the matrix. But in the second one, we can see the sorted array. Since we passed the axis “1”, it hasn’t sorted the complete array but it sorted it row-wise as displayed. Each row is sorted. The first row in the given array is “8, 1, and 7”. While in the sorted array, the first row is “1, 7 and 8”. Same as this, each row is sorted.

Method 2: Apply Over the Axis

In the given syntax, we have numpy.apply_over_axis function which is responsible for applying the function on the given axis. Inside the apply_over_axis function, we pass three arguments. The first one is the function that is to be performed. The second one is the array itself. And the last one is the axis on which we want to apply the function.

Example 2:

In the following instance, we perform the second method of the “apply” function in which we calculate the sum of the three-dimensional array. One thing to remember is that the sum of two arrays doesn’t mean we calculate the whole array. In some of the arrays, we calculate the row-wise sum which means that we add the rows and get the single element out of them.

Let’s move forward to our code. We first import the NumPy package and then create a variable that holds the three-dimensional array. In our case, the variable is “arr”. In the next line, we create another variable that holds the apply_over_axis function’s resulting array. We assign the apply_over_Axis function to the variable “arr” with three arguments. The first argument is the NumPy’s built-in function to calculate the sum which is np.sum. The second parameter is the array itself. The third argument is the axis over which the function is applied, in this case we have “[0, 2]” axis. At the end of the code, we execute both arrays using the print() statement.

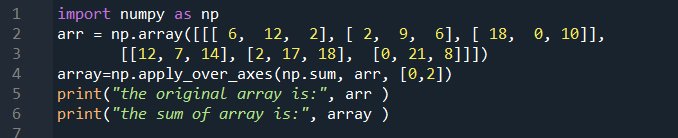
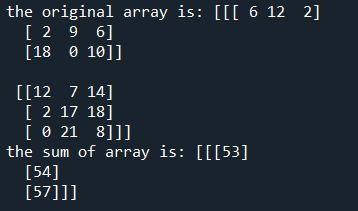
As shown in the following figure, we calculated some of our three-dimensional arrays using the apply_over_axis function. The first displayed array is the original array with the shape of “2, 3, 3” and the second one is the sum of the rows. The first-row sum is “53”, the second one is “54” and the last one is “57”.

Conclusion

In this article, we studied how the apply function is used in NumPy and how we can apply the different functions on arrays along or over the axis. It is easy to apply any function on the desired row or column by slicing them using the “apply” methods provided by NumPy. It is an efficient way when we don’t have to apply it to the whole array. We hope you find this post beneficial in learning how to utilize the apply method.