Complex Numbers in Python
“Complex Numbers” are a fundamental part of mathematics and engineering that provide a way to represent quantities that cannot be described using real numbers. In Python, complex numbers are treated as a separate data type, thereby allowing users to perform a wide range of complex number operations conveniently.
This article provides a complete guide on Python “Complex Numbers” using appropriate examples:
Data Type and Syntax of Complex Numbers
In Python, complex numbers are represented using the “complex” data type, which consists of a “real” and an “imaginary” component. The real component is denoted by “a”, while the imaginary component is denoted by “b”, as follows:
How to Create Complex Numbers in Python?
To create a complex number in Python, use the “complex()” function, which takes two arguments: the “real” component and the “imaginary” component. For example, to create the complex number “2 + 3j”, write the following code statement:
print(z)
In the above code, the “complex()” function is used to create the discussed complex number.
Output
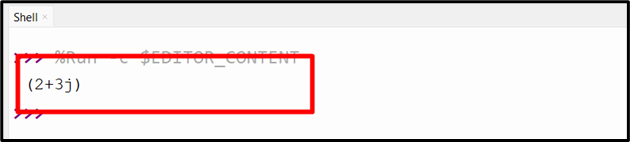
As seen, the corresponding complex number has been created successfully.
Example 1: Applying Basic Arithmetic Operations on Complex Numbers
Complex numbers can undergo all the fundamental arithmetic operations in Python, such as addition, subtraction, multiplication, and division. For example, to add two complex numbers “z1” and “z2”, you can use the below code:
z2 = complex(4, 5)
z3 = z1 + z2
print(z3)
In the above code, the two complex numbers are added using the concatenation operator “+”.
Output
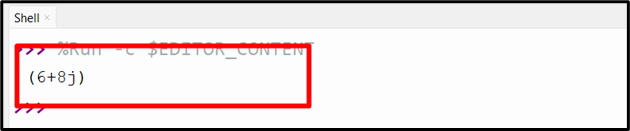
In the above snippet, both the complex numbers have been added successfully.
Example 2: Converting Complex Numbers Between Polar and Rectangular Forms
“Python has built-in functions that can change complex numbers from one form to another: either “polar” or “rectangular”. To convert a rectangular form of complex number “z” to polar form, use the “cmath.phase()” function, which retrieves the magnitude and phase angle of the input complex number.
To convert the input complex number “z” from polar to rectangular form instead, use the “cmath.rect()” function, which takes the magnitude and phase angle as a parameter. Here is an example code:
# Rectangular form
z_rect = complex(3, 4)
print(f"Rectangular form: {z_rect}")
# Polar form
r = abs(z_rect)
phi = cmath.phase(z_rect)
print(f"Polar form: ({r}, {phi})")
# Converting back to rectangular form
z_rect_2 = cmath.rect(r, phi)
print(f"Rectangular form again: {z_rect_2}")
In the above code, the “abs()” and “cmath.phase()” functions are used to convert/transform the input complex number into polar form. After that, the “cmath.rect()” function converts this from polar to rectangular.
Output
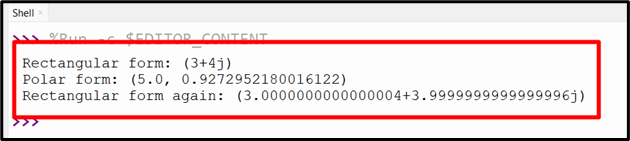
The rectangular form is converted into polar form and back to the rectangular form in the above output.
Example 3: Computing the Square Root of an Input Complex Number
Python provides a “cmath.sqrt()” function to calculate the square root of a complex number demonstrated below:
z = complex(4, 3)
w = cmath.sqrt(z)
print(w)
In this code, the “cmath.sqrt()” function retrieves the square root of the input complex number.
Output
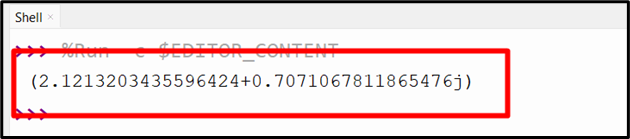
The above snippet shows the square root of the complex number.
Example 4: Calculating the Exponential of a Complex Number
The “cmath.exp()” function in Python can be used to calculate the exponential of a complex number as follows:
z = complex(2, 3)
w = cmath.exp(z)
print(w)
According to this code, the “cmath.exp()” function is utilized to find the “exponential” of the input complex number.
Output

The above snippet shows the exponential of a complex number.
Example 5: Complex Trigonometric Functions
Python provides a range of complex trigonometric functions, including “cmath.sin()”, “cmath.cos()”, “cmath.tan()”, “cmath.asin()”, “cmath.acos()”, and “cmath.atan()”. These functions can be utilized to execute a wide range of complex number operations, including solving equations and analyzing signals. For instance, the below code uses the “cmath.sin()” function to calculate the sine of a complex number:
z = complex(3, 4)
sin_z = cmath.sin(z)
print(sin_z)
In the above code, the “cmat.sin()” function calculates the sine of the given complex number in Python.
Output
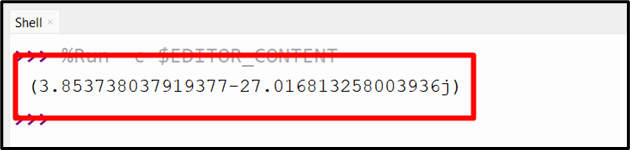
This output implies that the sine of the provided complex number has been calculated appropriately.
Conclusion
To summarize, “complex numbers” are an essential component of both mathematics and engineering as they enable the representation of quantities that cannot be described solely with real numbers. In Python, complex numbers are treated as a distinct data type that enables the users to carry out complex number operations with ease. This Python guide presented a comprehensive tutorial on “complex numbers”.
Source: linuxhint.com
