“Hamming distance” is an important concept in coding that calculates the difference between two binary strings. In other words, it is the number of positions where the corresponding symbols differ. It is widely used in error detection and correction, DNA sequencing, and cryptography. In this Python blog, we will discuss what Hamming distance is, and how to calculate it in Python using numerous examples.

How to Calculate Python Hamming Distance?

Python provides the following ways to compute/determine the Hamming distance between two strings:

• Using the Built-in Function “hamming()”.
• Via “Loops”.
• Using “List Comprehension”.

Method 1: Calculate Hamming Distance in Python Using the Built-in Function “hamming()”

The built-in function “hamming()” from the “scipy.spatial.distance” module is used to calculate the Hamming distance in Python. This function accepts two arrays as a parameter and returns their Hamming distance.

Syntax

Example
Let’s overview the following example code:

In the above code:

• The “hamming” function is imported from the “scipy.spatial.distance” module and the two arrays of binary data are initialized, respectively.
• After that, the “hamming()” function takes the two arrays as its arguments and calculates the Hamming distance between the two passed arrays comprising binary values.

Output

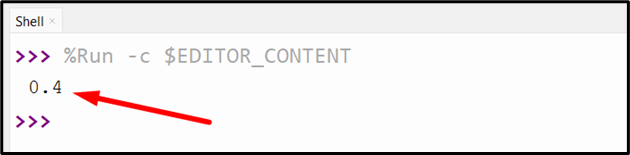
In the above output, the hamming distance between the two arrays of binary values has been calculated.

Note: In the above example, the “hamming()” function returned the value of “0.4”. This value cannot be interpreted because the value yields the “proportion” of different values. To find out how many items are different, we need to multiply the length of the array by the number of items.

Example
The below-given example explains the stated concept:

In this code snippet, the hamming distance between these two arrays is calculated using the “hamming()” function, and then multiplied by the length of the former array to get the total number of different elements between them(arrays).

Output

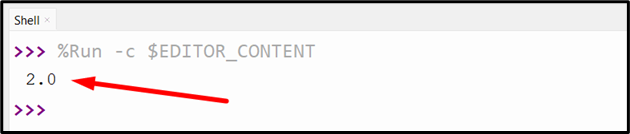
The hamming distance has been calculated appropriately in the above outcome.

Note: The reason for multiplying the result by the length of the input vectors is to normalize the Hamming distance by the length of the vectors, which gives us a value between “0” and “1”.

Method 2: Calculate Hamming Distance in Python Via Loops

Another way to calculate “Hamming” distance is by using “loops”. We can compare the corresponding symbols in the two strings and count the number of differences.

Example
The following code example will give you a quick overview:

In the above code block:

• The user-defined function named “hamming_distance()” is defined.
• This function accepts two strings as an argument and retrieves the “Hamming” distance between them.
• The Hamming distance is calculated by comparing each corresponding character in both the passed strings and counting the number of positions where they differ.
• After defining the function, the two strings containing binary values are initialized.
• Lastly, the user-defined function is invoked by giving the two strings as arguments.

Output

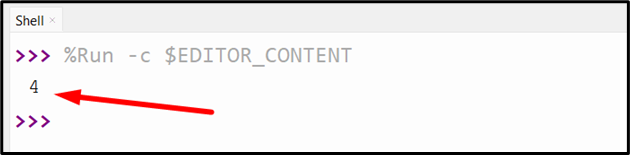
The hamming distance between two binary strings has been computed successfully in the above code snippet.

Method 3: Calculate Hamming Distance in Python Using “List Comprehension”

We can also calculate “Hamming” distance using “List Comprehension”. The method described here is more straightforward and elegant than loops.

Example
Here is the code:

According to the above lines of code:

• The two binary strings have been initialized in the program.
• The “List Comprehension” approach is applied to compare each pair of characters in both the strings and counts the number of positions where they differ.
• The “zip()” function is used to pair up the characters in both the strings at the same position.
• The condition “if i != j” checks if the two characters are different. If so, the value “1” is appended to the list.
• Finally, the “sum()” function adds up all the “1’s” in the list to analyze and give us the total number of positions where the strings differ.

Output

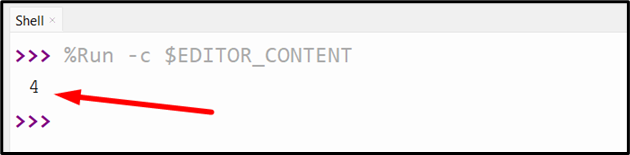
The above outcome implies that the hamming distance has been calculated successfully.

Conclusion

To calculate the “hamming distance” in Python, various methods such as using the built-in function “hamming()”, “loops”, or “List Comprehension” can be used. Hamming distance is an essential concept in coding and has numerous applications in different fields. This post presented various ways to determine the Python hamming distance using appropriate examples.